Simplifying Square Roots that Contain Variables
If you are looking to simplify square roots that contain numerals as the radicand, then visit our page on how to simplify square roots.
In this lesson, we are going to take it one step further, and simplify square roots that contain variables.
Here's What You'll Find On This Page:
Square Roots with Just One Variable
When you take the square root of a term that is "squared", your answer is the " base" of that term. Here's what I mean.
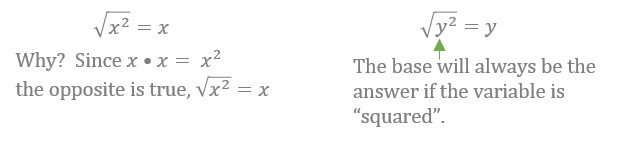
So, what happens if the variable is raised to a power other than 2?
Did you see how we rewrote the radicand but still maintained its value? Let's look at another example where a variable is raised to the sixth power.
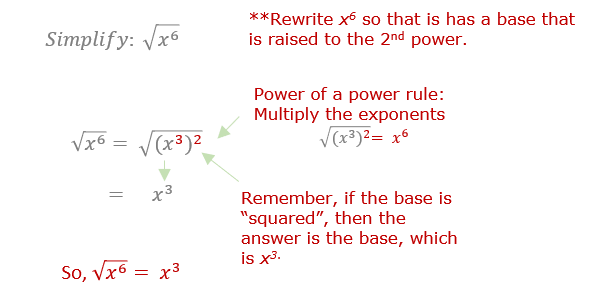
Now, let's look at a simplifying a square root that contains the product of a number and a variable.
Simplifying the Square Root of the Product of a Number and a Variable.
Let's look at another example where we simplify the square root of multiple factors. Take note of the variable z in this example. It must remain under the square root since it is z to the first power.
More Simplifying Square Roots with Multiple Variables
One last example. If you have a variable that is raised to an odd power, you must rewrite it as the product of two squares - one with an even exponent and the other to the first power. Check out the variable x in this example.
Simplifying Square Roots


Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
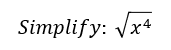
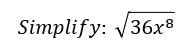
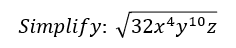
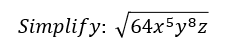

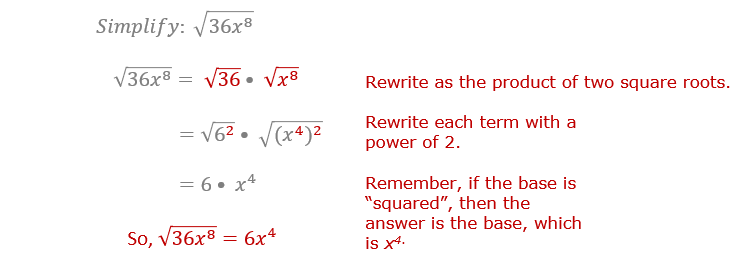
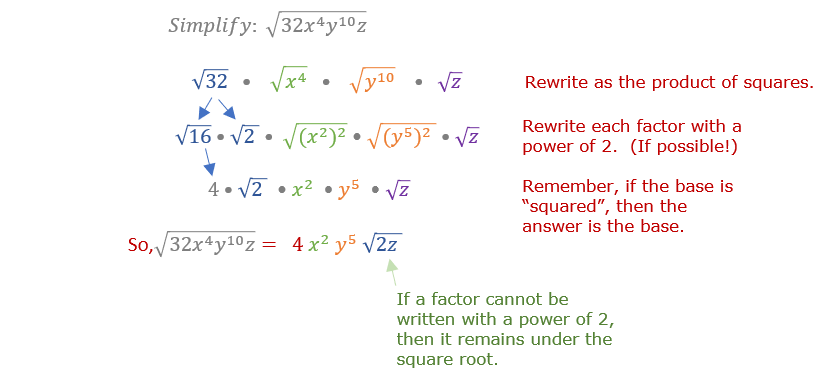





Comments
We would love to hear what you have to say about this page!