How To Find the Slope Given Two Points
Are you faced with the task of finding the slope of a line that passes through two particular points?
If so, what do you do?
- You could graph the two points and count the slope on the graph. This would work, but what if you don't have graph paper?
- You can use the slope formula to find the slope of two points.
What is the Slope Formula?
The slope formula is used to calculate the slope if you are given two points.
Remember that slope is defined as rise/run. Which translates to the rise divided by the run.
The slope formula will allow us to take the change in the rise and divide by the change in the run.
Take a look...
We will start with our two points. In order to define a generic formula, we must be able to label our two points. We will use subscripts to differentiate between the first point and the second point.
Now let's see how these points apply to the slope formula.
The Slope Formula
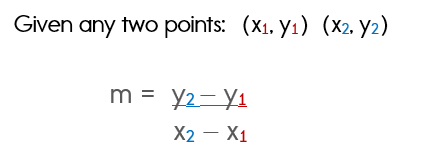
Notice how the formula directs us to subtract the two y values and divide that by the difference of the two x values. That's all there is to it!
In case you aren't familiar with slope intercept form, the "m" refers to the slope.
Let's take a look at an example to see how it is used.
Example 1: How to Find the Slope of Two Points
The most important thing to remember is that you must clearly identify each of the points as point 1 and point 2. As you substitute into the formula, make sure you substitute the correct coordinate.
I hope this helps you to understand how to find the slope using the slope formula. In the next lesson, you will apply this formula to solve rate of change problems.
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.