Are You Ready to Evaluate Algebraic Expressions?

In the past, you've evaluated numerical expressions by using the order of operations. We are going to use these same rules to evaluate algebraic expressions.


What is an Algebraic Expression?

An Algebraic expression is an expression that you will see most often once you start Algebra. In Algebra we work with variables and numerals.

A variable is a symbol, usually a letter, that represents one or more numbers.

Thus, an algebraic expression consists of numbers, variables, and operations.



Examples of Algebraic Expressions

An algebraic expression consists of numbers, variables, and operations. Here are a few examples:


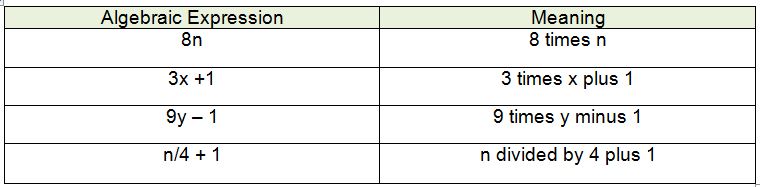
In order to evaluate an algebraic expression, you must know the exact values for each variable. Then you will simply substitute and evaluate using the order of operations. Take a look at example 1.


Example 1 - Evaluating Algebraic Expressions


Now, lets evaluate algebraic expressions with more than one variable. Don't forget to always use the order of operations when evaluating the expression after substituting.


Example 2 - Expressions with More Than One      Variable


And... one last example where we will look at the fraction bar as a grouping symbol and evaluating the expression when you have more than one of the same variable.


Example 3 - Using the Fraction Bar as a Grouping Symbol


If you are familiar with the order of operations, then evaluating algebraic expressions is quite easy! Just remember to substitute the given values for each variable and evaluate.

The next lesson in this unit is translating algebraic expressions.



  • Evaluate Expressions

    • Comments

    We would love to hear what you have to say about this page!

    Need More Help With Your Algebra Studies?

    Get access to hundreds of video examples and practice problems with your subscription! 

    Click here for more information on our affordable subscription options.

    Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.