Equations with Absolute Value:
Lesson 2 of 2

Solving equations with absolute value is a more advanced skill. However, with these step by step examples, you will have no problem mastering this skill.

If you haven't already studied the first lesson on solving absolute value equations, please start there to learn the basics.

Let's Recap. From that first lesson, you will need to remember the following:


Solving Absolute Value Equations

  • For most absolute value equations, you will need to write two equations to solve. Therefore, you will most likely end up with two answers to the equation.
  • The answer to an absolute value equation can never be negative. Therefore, if you end up with a scenario such as: |x-4| = -3, the answer to this would be the empty set.

One more important piece of information that you must remember is:

It's very important to check your answers to all absolute value equations because even if the correct procedure is used, the answers may not be solutions to the equation.

Take a look at the following example, which will demonstrate how only one solution is the correct answer to the actual equation.


Example 1 - One Solution

Pay careful attention to how we arrive at only one solution in this example.

Solving Absolute Value Equations
Verifying answers to absolute value equations


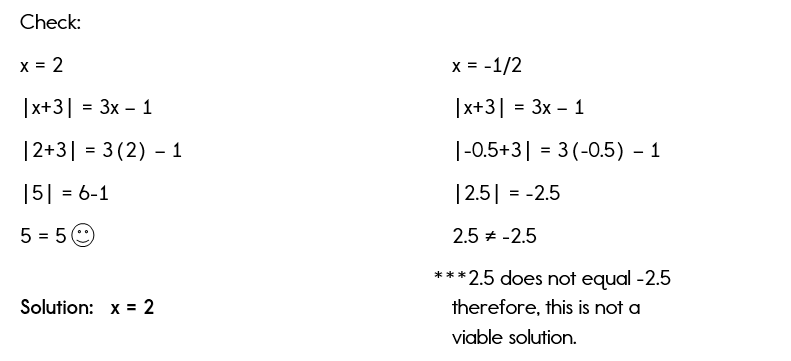
Ok, so now you understand why you must check your answers to every equation with absolute value.

You never know when one of those solutions is not going to be an actual solution to the equation.

Now we are going to take a look at another example that is a little more complex.

There is yet another rule that you must remember when solving absolute value equations. This new rule is:


Before you split the equation into two equations, you must make sure that the absolute value expression is by itself on one side of the equation.

This will be better understood with an example. Take a look...


Absolute Value examples

So, now let's take a look to see what we will need to do in order to isolate the absolute value on one side of the equation in order to prepare for solving the equation.

Watch carefully to see what step I take first in solving this equation.


Example 2 - Isolating the Absolute Value

Isolating the absolute value when solving equations
Checking absolute value solutions


Hopefully you were able to understand why we had to add 5 to both sides of the equation before writing our two equations.

The absolute value MUST be by itself on one side of the equation before splitting into two equations.

We are going to take a look at one more example.

This time we will need to divide in order to get the absolute value by itself on one side of the equation. Take a look....


Example 3 - Isolate the Absolute Value

Solving absolute value equations
Checking solutions to absolute value equations


In this lesson, I hope that you have realized that you must isolate the absolute value expression before writing your two equations.

I'm hoping that you also understand the importance of checking your answers to verify that the solutions are actual solutions to the equation.

Good luck in your study of equations.


  1. Home
    2. >
  2. Solving Equations
    3. >
  3. Absolute Value Equations



Comments

We would love to hear what you have to say about this page!

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.